Here are three little puzzles about infinity.

Here’s a short blue line and a red line that is 3x longer than the blue line. Let me show you how there are just as many points in the blue line as there are in the red line.

Let’s make a right triangle with the blue and red lines, and then draw a green line to connect them. I’ll draw a line connecting a point on the blue line to a point on the red line. I can draw an infinite number of lines from the blue line to the red line. Though the red line is three times longer than the blue line, they have an equal number of points.

The same idea works with circles. I have here two concentric circles. The bigger one has 3x the diameter of the small one, but they both have the same number of points.

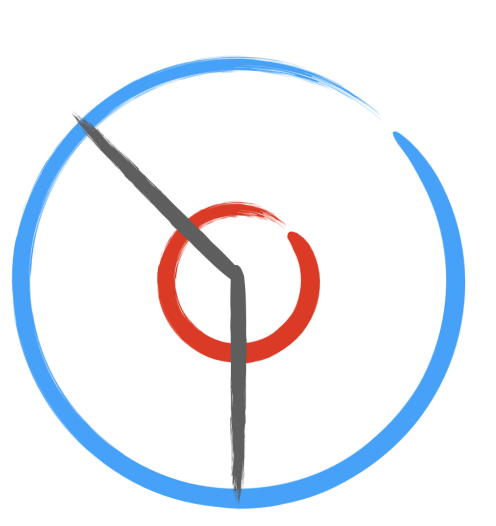
If I draw a line or two from the center, I trace a path over a point in the red circle and a corresponding point in the blue circle. The blue circle’s circumference might be 3x longer, but it has the same number of points as the red circle.

Here’s the last puzzle about infinity, but this time, I won’t give you the answer. Here’s a number line. This number line contains all the numbers from zero to infinity. There are an infinite number of numbers from zero to infinity. There are also an infinite number of numbers from 0 to 1 (e.g., 0.001, 0.000001, 0.0000000001, etc).

Which infinity is bigger? Is the infinity between 0 to 1 bigger than the infinity between 0 and ∞? Or vice-versa? Or are they the same size? And what does it mean to compare the size of one infinity to another?

I’ve always admired those who could grapple with pure math, the kind of math that doesn’t have a physical analog. I have a tough time of it. Pure math is about creating abstractions on top of abstractions. Very similar to computer programming, which has many, many layers of abstraction from assembly code to the networking protocols to the user interface.

Every once in a while, I come across a great book about pure math. I found these puzzles in David Foster Wallace’s Everything and More: A Compact History of Infinity. DFW simplifies some esoteric concepts about infinity and writes in a style that blends a deep understanding of math and philosophy with simplicity and humor. It’s hard to do, but a hugely successful effort. If you enjoy this kind of thing, it’s well worth a read.